Piano Key Frequency and Micro Tuning
Equal Temperament Tuning (Standard Tuning)
on a piano, each adjacent key (color doesn't matter), from left to right, their frequencies forms a geometric sequence. The scaling factor is 2^(1/12)≈1.05946.
Here's the standard tuning:

Micro Tuning
Micro tuning means change the pitch of each key so that the scaling is less than 2^(1/12).
here's a video of micro tuning.
Naming of the Keys
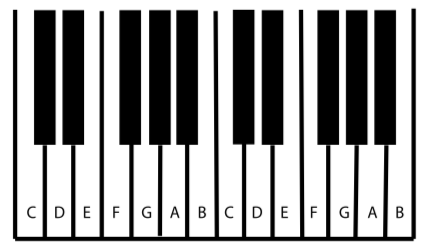
the white keys are labeled A B C to G. Starting with C on the left most white key of the 2 black keys group.
black keys don't have a name by themselfs, but is named relative to adjacent white keys. A black key to the right of a white key (say C) is called C♯ (sharp), or D♭ (flat). Basically, ♯ is used to jump to the right.
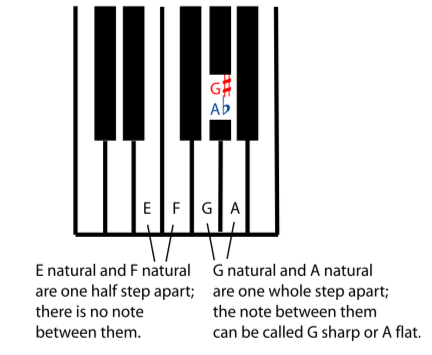
What is a Semitone (aka half-step), Whole Tone, Octave
- Semitone basically means adjacent keys. (color of the key doesn't matter.)
- A whole tone, is 2 semitones.
- An octave, is 12 semitones. in standard turing, it means the pitch frequency doubles or halves.
The Middle C Key and Concert A Key
move hand to somewhere in the middle and find the closest C key, that key is called Middle C, and find the A key above it. That A, is called Concert A. By standard tuning, that A key, has a frequency of 440Hz.
now, the western music scale is such that, every 12 intervals, the frequency doubles. So, when you find the middle A key (which has frequency 440Hz), the next A to the right, has frequency 880Hz.
since Bach's The Well-Tempered Clavier (1722), we have “equal temperament”
tuning.
Adjacent keys frequency differ by a constant multiplicative factor.
e.g.
Key A has frequency 440Hz.
The key right of it has frequency 440*c, where c is a constant.
then, next to it is
440*c*c ,
then, next to it is
440*c*c*c,
etc
, till 12 keys after it we have
440*c^12
, and should be 880Hz.
440*c^12==880
.
So
c = 2^(1/12)
Why the Black Keys?
on a piano, you might wonder why the black keys? why not all just white keys? well, lots history, but basically, the function of the current irregular shape (the 2/3 groups of black keys jutting out) is so that it's easier for fingers to find keys by touch.
on a piano, since key's frequencies is regular by a factor, why are they named irregularly C C# D D# E F F# G G# A A# B C. (those with # are black) Why not A to L? again, history. Like programing language syntax and math notations, most are result of hundreds years of habit, convention, from gradual evolution.